개요
- 패딩 오라클 취약점의 원리를 이해한 부분을 정리해둔다.
- padding oracle은 2002년에 Serge Vaudenay가 처음 발표하였고, 이후 이 공격을 응용한 다양한 취약점들이 발표되고 있다. 그 중 유명한 것으로 2014년에 구글 엔지니어팀이 발표한 POODLE (Padding Oracle On Downgraded Legacy Encryption)취약점이 있다.
- 이 취약점을 악용하면 CBC모드를 사용하는 블록암호에 있어서 특정 조건하에서 암호키 없이도 평문을 얻어내는 것이 가능하다.
- 내가 패딩 오라클 취약점을 처음 알게된 것은 2017년이다. 이 시점에 CVE 데이터베이스에서 padding oracle로 검색해보면 24건이 조회되었다.
- 2023년 7월에 다시한번 padding oracle로 검색해보니 50건이 조회되었다. 6년 사이에 26건이 추가된 것이다. 의외로 끊이지 않고 계속 발견되는 취약점이라는 것을 알 수 있다.
- 2024년 12월에는 53건 이었다.
사전지식
취약점을 이해하기 위해서 먼저 알아야 하는 개념을 정리한다. 패딩 오라클 취약점을 이해하려면 블록암호, 운용모드, 패딩 이렇게 세 가지에 대해서 개념을 잡고 있어야 한다.
블록암호
블록암호란 평문을 일정사이즈(블록)로 분할해서 블록별로 암호화 처리를 하는 방식이다. 대표적으로 DES, AES 가 블록암호 방식의 알고리즘이다. 블록의 사이즈는 보통 64비트(8바이트, DES)나 128비트(16바이트, AES)가 사용된다. 블록암호는 각 블록을 같은 암호키로 암호화했을 경우 해독이 쉬워진다는 단점이 있다. 그래서 처리를 복잡하게 하고 암호의 강도를 높이기 위해 운용 모드가 개발되었다.
운용모드
EBC, CBC, CFB, OFB 등 다양한 운용모드가 있지만 여기서는 EBC와 CBC 모드에 대해서만 설명한다.
ECB 모드
Electronic Code Book 의 약자로 평문을 블록으로 나눠서 각 블록을 암호화하는 방식이다. 각 블록이 독립적이므로 병행처리가 가능해 속도는 빠르지만 암호강도가 낮아서 사용하면 안되는 방식이다.
이미지 출처: en.wikipedia.org/wiki/Block_cipher_mode_of_operation
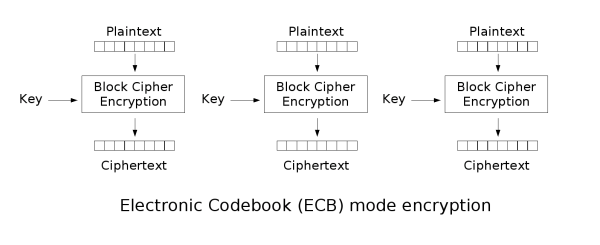
이미지를 ECB 모드로 암호화했을 경우 다음과 같이 이미지의 윤곽이 그대로 보이게 된다. 이 것으로 ECB 모드의 암호화 강도는 낮다는 것을 알 수 있다.

CBC 모드
Cipher Block Chaining 의 약자로 이전의 평문 블록의 암호결과와 다음 평문블록을 XOR한 결과를 암호화하는 방식이다. 1976년 IBM이 개발하였고, 첫번째 블록의 암호화에는 초기화 벡터(Initial Vector, IV)가 쓰인다. 초기화 벡터는 첫번째 블록의 입력 값으로 쓰이다. 암호의 강도가 높고, 널리 사용되고 있는 방식이다.
이미지 출처: https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation
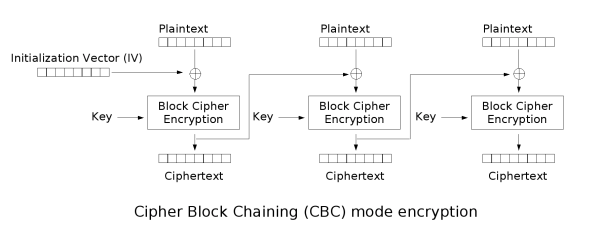
패딩
패딩은 평문의 마지막 블록에서 블록 사이즈에 비해 모자란 부분을 채워주는 값이다. 예를 들어 블록 사이즈가 8바이트이고, 평문이 5바이트라면 3바이트를 패딩으로 채워주는 식이다. 다양한 운용모드 중에서 ECB, CBC 모드가 패딩을 사용한다. (이 모드들은 평문의 크기가 블록 사이즈의 배수여야 한다는 규칙이 있기 때문에 패딩을 사용한다.)
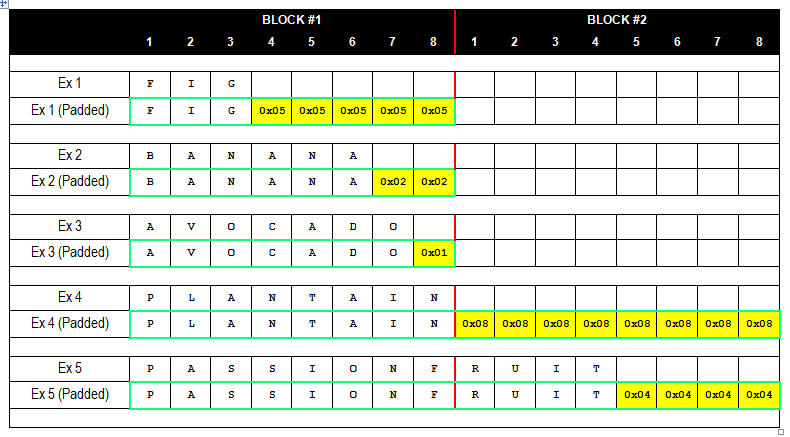
PKCS#7
패딩은 여러가지 종류가 있지만 블록 암호에서는 PKCS#7 를 사용한다. 다음 그림이 8바이트 블록 암호화에서 패딩의 개념을 보여주고 있다. PKCS#7 패딩의 규칙은 패딩의 개수(바이트수)와 그 값이 일치해야 한다는 것이다. 예를 들어 패딩이 한 개일 경우는 패딩의 값도 0x01, 패딩이 두 개인 경우는 패딩의 값도 0x02 여야한다. 평문의 크기가 블록 크기와 동일한 경우는 어떨까? 그림에서 Ex4를 보면 8바이트 블록과 동일한 사이즈인 경우 8개의 패딩이 추가되는 것을 볼 수 있다. 이 것으로 평문과 블록이 동일한 사이즈인 경우에도 패딩이 추가된다는 것을 알 수 있다.
이미지 출처: https://blog.gdssecurity.com/labs/2010/9/14/automated-padding-oracle-attacks-with-padbuster.html
취약한 서버 사양
취약점의 원리를 설명하기 위해 다음과 같은 서버가 존재한다고 가정한다.
- 이 서버에는 요청을 보내면 평문을 암호화하거나, 또는 암호화된 값을 복호화해주는 기능이 있다.
- 이 서버는 복호화에 성공하면 복호화된 평문을 회신해준다.
- 이 서버는 복호화에 실패해서 에러가 발생하면 에러를 그대로 회신해준다.
- 이 서버는 암호 알고리즘으로 8바이트 블록을 사용하는 3DES를 사용한다.
- 결과적으로 이 서버에는 패딩 오라클 취약점이 있다.
시나리오
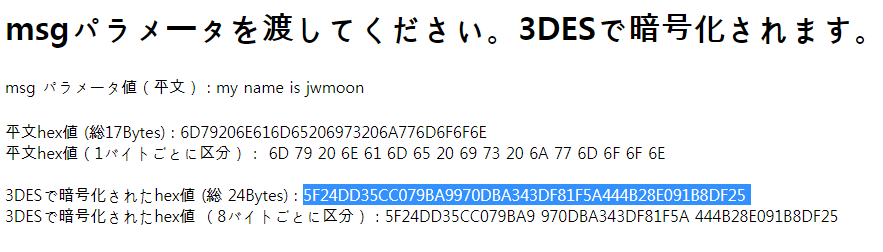
이 서버에 평문 ‘my name is jwmoon’을 보냈더니 24바이트 암호문 ‘5F24DD35CC079BA9970DBA343DF81F5A444B28E091B8DF25’ 을 회신해주었다. 이 암호문을 패딩 오라클 취약점을 이용해서 풀어본다.
이해의 편의를 위해 헥스 값을 문자열로 변환해서 표현했다. 헥스 값 2개가 1 바이트를 의미한다.
공격 수행
패딩 오라클이 어떤 원리로 암호화된 값의 평문을 얻어내는지를 이해하기 위해서는 두 가지 단계를 “제대로” 이해해야 한다. 두 단계는 복호화 과정과 패딩 규칙이다.
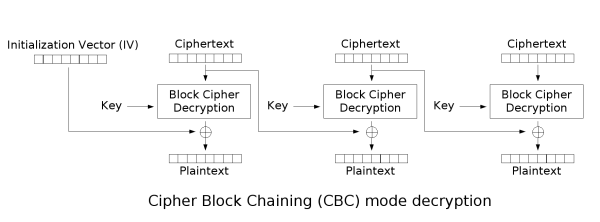
필수이해1: 복호화 과정
원리를 이해하기 위한 첫번째 단계는 CBC모드의 복호화 과정을 확실하게 이해하는 것이다.
복호화 과정을 다시 한번 살펴본다.

위의 복호화 과정을 예제 암호문의 복호화 과정에 적용해서 표현해보자.
“my name is jwmoon” 을 암호화한 값 5F24DD35CC079BA9970DBA343DF81F5A444B28E091B8DF25 을 8바이트 단위로 쪼개면 다음과 같다.
5F24DD35CC079BA9 970DBA343DF81F5A 444B28E091B8DF25
그리고 CBC모드의 복호화 처리 프로세스대로 표현하면 다음과 같이 된다.
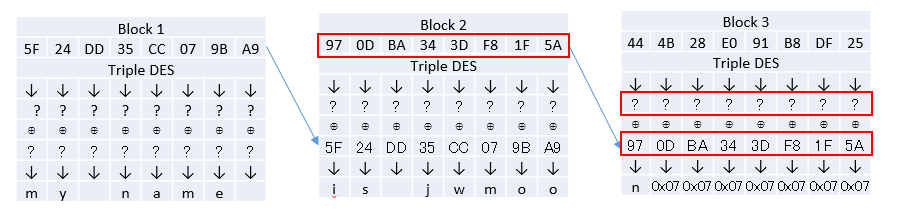
그림의 첫번째 블록(Block 1)을 살펴보자.
- 가장 위쪽에 위치한 부분은 암호화된 바이트값을 나타낸다.
- Triple DES라고 표기된 부분을 복호화가 수행되는 것을 나타낸다.
- 복호화가 수행된 후의 값을 알 수 없으므로 물음표로 표현되었다.
- 복호화된 값과 이니셜 벡터(IV)의 값을 XOR한 결과가 my name 이라는 평문으로 표시되었다.
CBC 모드 복호화 과정의 특징은 이전 블록의 암호화된 값이 다음 블록의 복호화에 사용된다는 것이다. 더 구체적으로는 이전 블록의 암호화된 값과 현재 블록의 복호화된 값을 XOR한 값 이 현재 블록의 평문이 된다는 것이다.
예를 들어 그림에서 Block3의 평문 값은 Block2의 값 8바이트 970DBA343DF81F5A과 Block 3의 복호화된 값 8바이트 ???????? 를 XOR 한 값이다.
따라서 이전 블록의 특정 위치의 바이트 값을 변경하면 다음 블록의 동일한 위치의 바이트의 평문값에 영향을 미친다 는 것을 추론할 수 있다. 예를 들어 Block 2에서 암호화된 바이트의 마지막 값인 5A를 변경하면 Block 3의 평문의 마지막 바이트값에 영향을 미치게 된다.
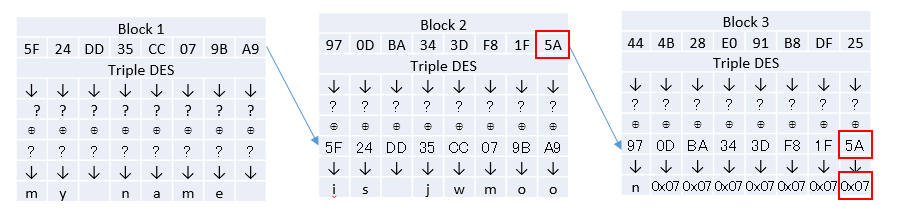
필수이해2: 패딩 규칙
공격을 이해하기 위한 두 번째 단계는 패딩의 규칙을 이해하는 것이다. 위의 그림에서 Block3의 평문 값을 보면 뒤의 일곱 바이트의 값이 헥스 값 07로 채워져 있는 것을 볼 수 있다. 패딩 값은 블록 사이즈를 맞추기 위해 평문의 가장 뒤에 붙여주는 값이다. 이번 예제에서는 패딩의 개수가 7개이기 때문에 패딩의 값도 07로 되어 있다. 패딩의 값과 수가 맞지 않거나 패딩 값이 가능한 범위(3DES는 8바이트 블록이므로 0x01~0x08)를 벗어나면 어떻게 될까? 복호화 도중에 오류가 발생하게 된다. 실습 환경인 jsp 환경에서는 다음과 같이 BadPaddingException 이 일어난다.
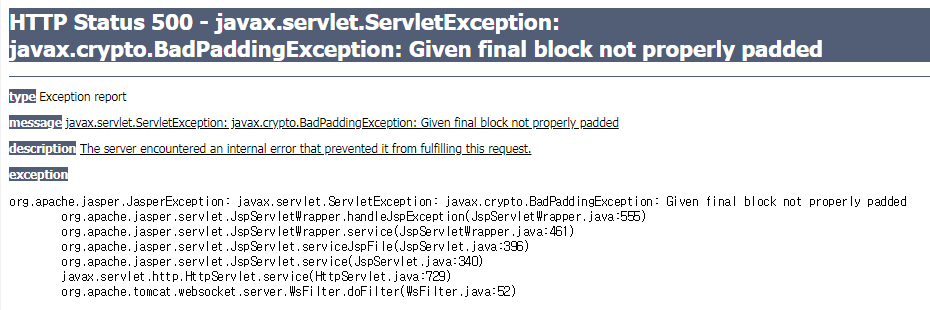
위의 규칙에 따라 알 수 있는 중요한 특징은 암호문의 내용에 상관없이 패딩의 규칙에만 맞으면 복호화 도중 에러를 발생시키지 않는다 는 것이다.
예를 들어 Block2 암호문 중 마지막 바이트를 어떤 값으로 수정한 후 Block3 의 복호화를 시도했더니 평문의 마지막 바이트 값이 0x01이 나왔다고 상상해 보자. 이 경우 0x01은 패딩으로 사용가능한 값이고 또한 개수가 한 개 나왔으므로 패딩 규칙에 어긋나지 않으므로 에러가 발생하지 않는다. (실제로 복호화된 값은 사람이 알아볼 수 없는 값일 수도 있다)
참고로, 암호문의 길이가 바뀐 경우는 어떨가? 예를들어, 24바이트 암호문 ‘5F24DD35CC079BA9970DBA343DF81F5A444B28E091B8DF25’ 에서 앞의 8바이트를 뺀 나머지 16바이트 ‘970DBA343DF81F5A444B28E091B8DF25’만 복호화를 시도하면 어떻게 될까? 이 경우도 마찬가지로 패딩에러가 발생하지 않는다. 복호화되는 평문은 훼손되지만 패딩의 규칙에 어긋나지 않았기 때문이다. (다만 암호문의 길이는 블록 크기의 배수여야 한다는 규칙을 지켜야 한다. 예를들어 24바이트 암호문 중에서 4바이트를 잘라서 20바이트 암호문을 시도한다면 블록 사이즈인 8바이트의 배수가 아니기 때문에 암호문 길이가 잘못되었다는 에러가 발생한다.)
공격수행: 서버의 반응을 구별해서 중간 값을 획득하기
지금까지의 설명을 통해 암호문의 값에 따라 서버는 다음 세 가지 중 하나의 반응을 보일 것이라고 예상할 수 있다.
1) 암호문이 올바른 내용일 경우(복호화에도 문제가 없었고 평문도 올바르다): 200 ok 응답 2) 복호화 도중 오류발생: 500 error 응답 3) 복호화에는 문제없지만 잘못된 평문인 경우: 200 ok (어플리케이션 구현에 따라 커스텀 에러 메세지 가능성 있음)
그리고 위의 세 가지 반응을 구별하는 것으로 시도한 암호문의 패딩이 올바른지 여부를 알 수 있다. 참고로 이러한 서버의 반응을 암호학에서는 ‘오라클’ 이라고 부른다. 이번 취약점의 이름인 padding oracle 은 패딩 값에 따라 서버가 다르게 반응하는 것을 말한다.
패딩이 올바른 경우를 구분할 수 있게되면 중간값을 구할 수 있고, 결과적으로 평문의 값도 알 수 있게 된다. 예를 들어 다음 그림에서 붉은 색 상자로 표시된 부분을 보자. 앞으로 이 것을 Block3의 중간값이라고 부르자. 이 중간값을 얻어낼 수 있다면 어떻게 될까? 평문을 구할 수 있게 된다! 왜냐하면 복호화 과정에 따라 ‘중간 값 ⊕ 이전 블록의 암호문 = 현재 블록의 평문’ 인 것을 알고 있기 때문이다. (⊕ 표시는 XOR 연산을 의미한다) 이전 블록의 암호문은 이미 주어져 있고 중간 값도 알고 있기 때문에 XOR연산을 통해서 평문을 구할 수 있게 된다.
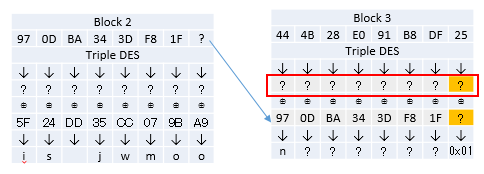
Block3의 중간값 블록의 마지막 바이트 구하기
이어서 중간값을 구하는 과정에 대해서 살펴보자. 중간값은 한번에 하나의 바이트 값만 얻어낼 수 있기 때문에 여러번의 시도가 필요하다. 가장 마지막 바이트부터 시작해서 그 앞의 바이트 값을 얻어내는 식으로 수행해 나간다.
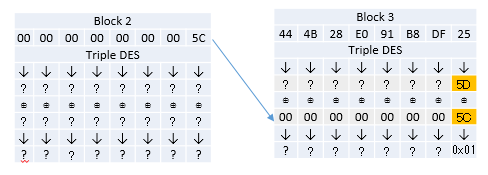
먼저 Block3 중간값 블록의 마지막 바이트를 구하는 과정을 보자. 시도할 암호문을 다음과 같이 바꾼 경우를 생각해보자.
- Block2의 암호문이 0x00000000000000?? 이 되었다.
00000000000000??444B28E091B8DF25
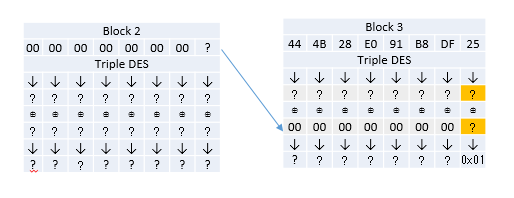
세번째 블록 값은 그대로이고 두번째 블록의 값을 모두 0으로 채운뒤 마지막 바이트를 가질 수 있는 값의 범위 (0x00~0xFF) 중에서 하나로 복호화를 시도해나간다. 대부분은 패딩에러가 발생하지만 결과나 0x01이 나오게 되면 에러가 발생하지 않는다. (0x01은 정당한 패딩의 값이다.)
값을 변경해보면서 시도해보면 값이 5C일 때 에러가 발생하지 않는 것을 알 수 있다.
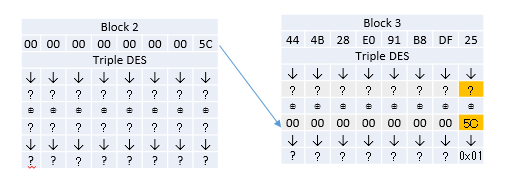
그러면 중간 값의 마지막 바이트는 어떻게 구할 수 있을까? XOR 성질을 이용하면 된다.
XOR의 진리값은 다음과 같다.
XOR 은 두 비트의 값이 같으면 0을, 다르면 1을 리턴한다.
이 것을 이용해 다음 두 개의 규칙을 도출할 수 있다.
- 어떤 비트열을 동일한 비트열로 XOR 연산하면 동일한 길이의 0으로 채워진 비트열을 얻는다.
- 어떤 비트열을 동일한 길이의 0으로 채워진 비트열과 XOR하면 원래의 비트열을 얻는다.
이 규칙을 염두에 두면서 다음 식을 보자. 마지막 바이트의 값을 X라고 했을 때 다음식이 도출된다.
X ⊕ 0x5C = 0x01
=> X ⊕ (0x5C ⊕ 0x5C) = 0x5C ⊕ 0x01
=> X ⊕(0x00) = 0x5C ⊕ 0x01
=> X = 0x5C ⊕ 0x01 = 0x5D
찾은 값(패딩 에러가 나오지 않은 값) 5C와 패딩 0x01을 XOR해서 중간 값 0x5D 를 얻었다!
Block3의 뒤에서 두번째 바이트 구하기
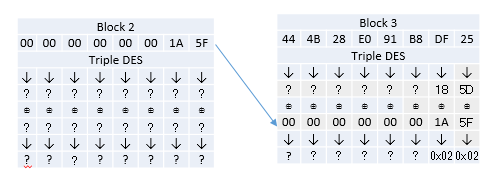
그러면 이어서 뒤에서 두번째의 바이트를 구해보자. 어떻게 구할 수 있을까?
Block2의 뒤의 두 바이트를 변경했을 때 복호화된 평문의 두 바이트의 값이 0x02가 되도록 하면 된다. 이 때 가장 마지막 바이트의 중간 값은 이전 단계에서 구해놓았으므로 시도하고자 하는 암호문의 마지막 바이트도 구할 수 있다. 다음 그림에서 노란색으로 칠해진 부분의 값은 0x5D와 0x02를 XOR해서 구할 수 있다. 그리고 그 값은 0x5F 다.


Block2 암호문의 마지막 바이트를 5F로 설정한 후 뒤에서 두번째 바이트를 0x00부터 0xFF까지 브루트 포스를 시도한다. 그리고 에러가 발생되지 않는 값을 찾는다.
찾아보니 그 값은 1A 다. 마지막 바이트 때와 마찬가지로 공식을 통해 중간 값을 찾아낸다. 중간 값은 0x18 다.
X ⊕ 0x1A = 0x02
X = 0x02 ⊕ 0x1A = 0x18
이렇게 해서 뒤에서 두번째 바이트의 중간 값도 찾았다.
같은 요령으로 Block3의 뒤에서 세번째 바이트를 구하고, 다음은 뒤에서 네번째 바이트… 그리고 마지막 바이트인 Block8의 첫번째 바이트까지 구하면 된다.
Block2의 중간값 구하기
Block3의 중간 값을 모두 구했다고 하자. Block2의 값은 어떻게 구할 수 있을까? Block3를 구했을 때와 마찬가지다. Block2의 암호문 값이 ‘970DBA343DF81F5A’ 이므로 Block1부분을 0으로 채운 ‘0000000000000000970DBA343DF81F5A’를 사용해서 Block1의 마지막 바이트부터 바꿔가면서 찾으면 된다.
자동화 프로그램
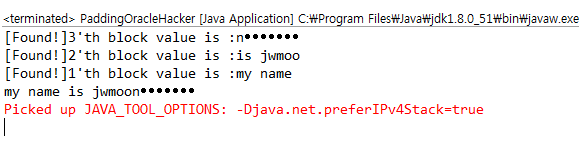
지금까지 설명한 과정을 사람 손으로 일일히 시도하게 되면 시간이 오래걸리지만 프로그램을 만들어서 자동화하면 금방 구할 수 있다. 한 바이트의 값을 알아내기 위해서 최대 256번 브루트 포스를 수행하면 하나의 바이트의 값을 알아낼 수 있다. 예를 들어 24바이트의 암호문이라면 최대 6144 번의 요청(24 x 256 = 6144)으로 평문을 알아낼 수 있다. 자동화 프로그램으로 알아낸 평문은 다음과 같다. padding oracle 공격으로 평문을 완벽하게 얻어낸 것을 알 수 있다.
방어방법
그러면 방어 방법을 알아보자. padding oracle 공격이 성공하기 위한 전제조건을 다시 한번 생각해보면 다음과 같다.
- 사용자가 암호문을 마음대로 바꿔서 보내도 서버는 복호화를 시도한다.
- 서버에서 복호화 에러가 발생할 경우 그 것을 알려준다.
거꾸로 말하면 이 전제조건이 성립되지 않으면 공격이 통하지 않는다고 볼 수 있다. 그렇게 하기 위해서 다음과 같은 방법을 사용할 수 있다.
암호문 정당성 검증 메커니즘 추가
MAC(Message Authentication Code)을 도입한다. 암호문에 MAC을 함께 보내도록하고 MAC의 정당성(변조여부)을 검증한 뒤에 정당한 암호문인 경우만 복호화를 시도한다. 이 때 MAC은 항상 암호문에 대한 MAC(encrypt-then-MAC)을 사용하는 것이 좋다.
에러 메세지 동일화
복호화 시에 발생할 수 있는 다양한 에러에 대해 보다 일반적인 에러 메세지로 바꿔서 회신한다. 그래서 공격자 입장에서 방금 시도한 암호문의 성공여부를 판단하기 어렵게 한다.
마치며
padding oracle 공격은 앞서 설명한 것처럼 암호 알고리즘 자체보다는 암호 알고리즘을 사용해서 서비스를 하는 서버의 응답을 이용하므로 일종의 사이드 채널(side channel)공격이라고 할 수도 있다. 암호키 없이도 평문을 알아낼 수 있으므로 이 취약점이 있는 경우 개인정보나 비밀번호와 같은 중요 정보가 노출될 수 있다.
padding oracle 공격은 CVE 데이터베이스에서 찾아보면 2024년 12월기준 53건 이 조회된다. (2017년에는 24건 이었다. 매년 3~4건 정도 보고되고 있다.) 건수는 많지 않으나 그 내용을 살펴보면 OpenSSL처럼 널리 사용되는 암호화 통신 라이브러리에서 보고되는 등 영향 범위는 넓다고 볼 수 있다. 또한 POODLE이나 RSA padding oracle(ROBOT)과 같은 응용 공격도 보고되고 있다. 따라서 취약점이 발표된 라이브러리는 최대한 빠르게 업데이트하는 것이 필요하다.
또한 어플리케이션 레벨에서 블록암호를 사용할 경우엔 앞서 설명한 바와 같이 padding oracle 공격이 통하지 않도록 구현하는 것이 중요하다.
참고자료
- wikipedia(padding oracle): https://en.wikipedia.org/wiki/Padding_oracle_attack
- wikipedia (block cipher mode) : https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation
- hacker 101 : https://www.hacker101.com/vulnerabilities/padding_oracle
- padding oracle attack by laughfool : http://laughfool.tistory.com/31
- 일본 정보처리안전보호지원사 2017 수험서
- gdssecurity: https://blog.gdssecurity.com/labs/2010/9/14/automated-padding-oracle-attacks-with-padbuster.html
추기
- 패딩 오라클 공격의 변형인 Lucky Thirteen 공격이 있다는 것을 알게 되었다.(https://en.wikipedia.org/wiki/Lucky_Thirteen_attack)